Pearson correlation coefficient

Not to be confused with Coefficient of determination.

Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. The correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.

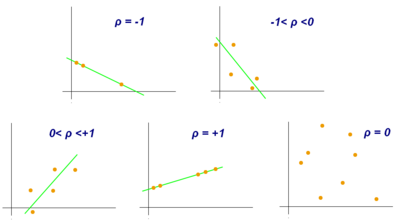
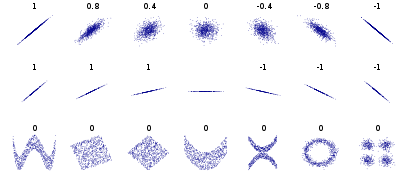
In statistics, the Pearson correlation coefficient (PCC)[a] is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a primary school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).

  1. ^ "SPSS Tutorials: Pearson Correlation".
  2. ^ "Correlation Coefficient: Simple Definition, Formula, Easy Steps". Statistics How To.


Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).