This article includes a list of general references, but it lacks sufficient corresponding inline citations. (February 2008) |
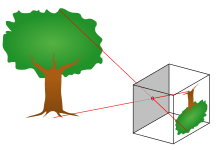
The pinhole camera model describes the mathematical relationship between the coordinates of a point in three-dimensional space and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light. The model does not include, for example, geometric distortions or blurring of unfocused objects caused by lenses and finite sized apertures.[1] It also does not take into account that most practical cameras have only discrete image coordinates. This means that the pinhole camera model can only be used as a first order approximation of the mapping from a 3D scene to a 2D image. Its validity depends on the quality of the camera and, in general, decreases from the center of the image to the edges as lens distortion effects increase.
Some of the effects that the pinhole camera model does not take into account can be compensated, for example by applying suitable coordinate transformations on the image coordinates; other effects are sufficiently small to be neglected if a high quality camera is used. This means that the pinhole camera model often can be used as a reasonable description of how a camera depicts a 3D scene, for example in computer vision and computer graphics.
- ^ Szeliski, Richard (2022). Computer Vision: Algorithms and Applications (2 ed.). Springer Nature. p. 74. ISBN 3030343723. Retrieved 30 December 2023.