Polytope families

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Polytope families" – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this message)

This page or section uses colour as the only way to convey important information. To meet Wikipedia's web accessibility guidelines, please help improve this page or section so it is easier to read by those with disabilities by adding an additional means for these readers to access the relevant information. See the guides to editing for accessibility at contrast and colours. (March 2021)

There are several families of symmetric polytopes with irreducible symmetry which have a member in more than one dimensionality. These are tabulated here with Petrie polygon projection graphs and Coxeter–Dynkin diagrams.

Table of irreducible polytope families
Family n	n-simplex	n-hypercube	n-orthoplex	n-demicube	1k2	2k1	k21	pentagonal polytope
Group	An	Bn		I2(p) Dn	E6 E7 E8 F4 G2			Hn
2	Triangle	Square		p-gon (example: p=7)	Hexagon			Pentagon
3	Tetrahedron	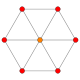Cube	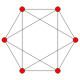Octahedron	Tetrahedron				Dodecahedron	Icosahedron
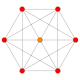4	5-cell	Tesseract	16-cell	Demitesseract	24-cell			120-cell	600-cell
5	5-simplex	5-cube	5-orthoplex	5-demicube
6	6-simplex	6-cube	6-orthoplex	6-demicube	122	221
7	7-simplex	7-cube	7-orthoplex	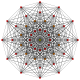7-demicube	132	231	321
8	8-simplex	8-cube	8-orthoplex	8-demicube	142	241	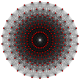421
9	9-simplex	9-cube	9-orthoplex	9-demicube
10	10-simplex	10-cube	10-orthoplex	10-demicube