The systems science portal
 |
| Complex systems approach |
Systems science is an transdisciplinary[1] field that studies the nature of systems—from simple to complex—in nature, society, cognition, engineering, technology and science itself. To systems scientists, the world can be understood as a system of systems. The field aims to develop interdisciplinary foundations that are applicable in a variety of areas, such as psychology, biology, medicine, communication, business management, engineering, and social sciences.
Systems science covers formal sciences such as complex systems, cybernetics, dynamical systems theory, information theory, linguistics or systems theory. It has applications in the field of the natural and social sciences and engineering, such as control theory, operations research, social systems theory, systems biology, system dynamics, human factors, systems ecology, systems engineering and systems psychology. Themes commonly stressed in system science are (a) holistic view, (b) interaction between a system and its embedding environment, and (c) complex (often subtle) trajectories of dynamic behavior that sometimes are stable (and thus reinforcing), while at various 'boundary conditions' can become wildly unstable (and thus destructive). Concerns about Earth-scale biosphere/geosphere dynamics is an example of the nature of problems to which systems science seeks to contribute meaningful insights.
Selected article -
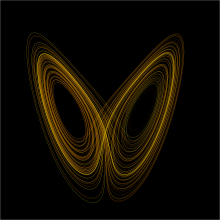
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.
At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manifold. The evolution rule of the dynamical system is a function that describes what future states follow from the current state. Often the function is deterministic, that is, for a given time interval only one future state follows from the current state. However, some systems are stochastic, in that random events also affect the evolution of the state variables. (Full article...)
Selected picture
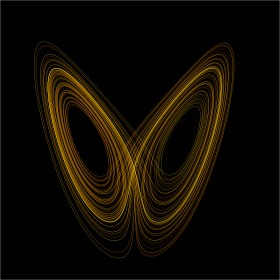
The Lorenz attractor is a 3-dimensional structure corresponding to the long-term behavior of a chaotic flow, noted for its butterfly shape. The map shows how the state of a dynamical system (the three variables of a three-dimensional system) evolves over time in a complex, non-repeating pattern.
The attractor itself, and the equations from which it is derived, were introduced by Edward Lorenz in 1963, who derived it from the simplified equations of convection rolls arising in the equations of the atmosphere.
'WikiProjects
Selected biography -
William Ross Ashby (6 September 1903 – 15 November 1972) was an English psychiatrist and a pioneer in cybernetics, the study of the science of communications and automatic control systems in both machines and living things. His first name was not used: he was known as Ross Ashby.
His two books, Design for a Brain and An Introduction to Cybernetics, introduced exact and logical thinking into the brand new discipline of cybernetics and were highly influential. These "missionary works" along with his technical contributions made Ashby "the major theoretician of cybernetics after Wiener". (Full article...)
Did you know
- ... that a successful experimental system must be stable and reproducible enough for scientists to make sense of the system's behavior, but unpredictable enough that it can produce useful results?
- ... that the American ecologist Howard T. Odum in 1950 gave a novel definition of ecology as the study of large entities (ecosystems) at the "natural level of integration".
- ... that the Yugoslavian Mihajlo D. Mesarovic in 1970s wanted to provide a unified and formalized mathematical approach to all major systems concepts.
- ... that the American systems scientist John Nelson Warfield found systems science to consist of a hierarchy of sciences.
Categories
Related portals
Topics
Tasks
 |
Here are some tasks awaiting attention:
|













