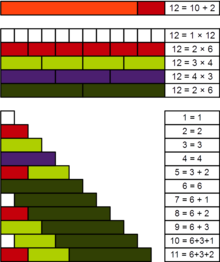
In number theory, a practical number or panarithmic number[1] is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.
The sequence of practical numbers (sequence A005153 in the OEIS) begins
Practical numbers were used by Fibonacci in his Liber Abaci (1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.[2]
The name "practical number" is due to Srinivasan (1948). He noted that "the subdivisions of money, weights, and measures involve numbers like 4, 12, 16, 20 and 28 which are usually supposed to be so inconvenient as to deserve replacement by powers of 10." His partial classification of these numbers was completed by Stewart (1954) and Sierpiński (1955). This characterization makes it possible to determine whether a number is practical by examining its prime factorization. Every even perfect number and every power of two is also a practical number.
Practical numbers have also been shown to be analogous with prime numbers in many of their properties.[3]
- ^ Margenstern (1991) cites Robinson (1979) and Heyworth (1980) for the name "panarithmic numbers".
- ^ Sigler (2002).
- ^ Hausman & Shapiro (1984); Margenstern (1991); Melfi (1996); Saias (1997).
