
In quantum mechanics, the quantum revival[1] is a periodic recurrence of the quantum wave function from its original form during the time evolution either many times in space as the multiple scaled fractions in the form of the initial wave function (fractional revival) or approximately or exactly to its original form from the beginning (full revival). The quantum wave function periodic in time exhibits therefore the full revival every period. The phenomenon of revivals is most readily observable for the wave functions being well localized wave packets at the beginning of the time evolution for example in the hydrogen atom. For Hydrogen, the fractional revivals show up as multiple angular Gaussian bumps around the circle drawn by the radial maximum of leading circular state component (that with the highest amplitude in the eigenstate expansion) of the original localized state and the full revival as the original Gaussian.[2] The full revivals are exact for the infinite quantum well, harmonic oscillator or the hydrogen atom, while for shorter times are approximate for the hydrogen atom and a lot of quantum systems.[3]
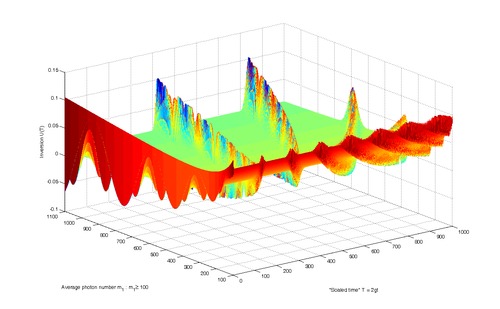
The plot of collapses and revivals of quantum oscillations of the JCM atomic inversion.[4]
- ^ J.H. Eberly; N.B. Narozhny & J.J. Sanchez-Mondragon (1980). "Periodic spontaneous collapse and revival in a simple quantum model". Phys. Rev. Lett. 44 (20): 1323–1326. Bibcode:1980PhRvL..44.1323E. doi:10.1103/PhysRevLett.44.1323.
- ^ Z. Dacic Gaeta & C. R. Stroud, Jr. (1990). "Classical and quantum mechanical dynamics of quasiclassical state of a hydrogen atom". Phys. Rev. A. 42 (11): 6308–6313. Bibcode:1990PhRvA..42.6308G. doi:10.1103/PhysRevA.42.6308. PMID 9903927.
- ^ Zhang, Jiang-Min; Haque, Masudul (2014). "Nonsmooth and level-resolved dynamics illustrated with a periodically driven tight binding model". Scienceopen Research. arXiv:1404.4280. doi:10.14293/S2199-1006.1.SOR-PHYS.A2CEM4.v1. S2CID 57487218.
- ^ A. A. Karatsuba; E. A. Karatsuba (2009). "A resummation formula for collapse and revival in the Jaynes–Cummings model". J. Phys. A: Math. Theor. 42 (19): 195304, 16. Bibcode:2009JPhA...42s5304K. doi:10.1088/1751-8113/42/19/195304. S2CID 120269208.