| Part of a series on statistics |
| Probability theory |
|---|
 |
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events.[1] The term 'random variable' in its mathematical definition refers to neither randomness nor variability[2] but instead is a mathematical function in which
- the domain is the set of possible outcomes in a sample space (e.g. the set which are the possible upper sides of a flipped coin heads or tails as the result from tossing a coin); and
- the range is a measurable space (e.g. corresponding to the domain above, the range might be the set if say heads mapped to -1 and mapped to 1). Typically, the range of a random variable is a subset of the real numbers.
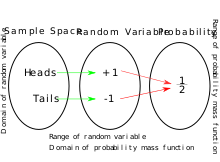
Informally, randomness typically represents some fundamental element of chance, such as in the roll of a die; it may also represent uncertainty, such as measurement error.[1] However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup.
In the formal mathematical language of measure theory, a random variable is defined as a measurable function from a probability measure space (called the sample space) to a measurable space. This allows consideration of the pushforward measure, which is called the distribution of the random variable; the distribution is thus a probability measure on the set of all possible values of the random variable. It is possible for two random variables to have identical distributions but to differ in significant ways; for instance, they may be independent.
It is common to consider the special cases of discrete random variables and absolutely continuous random variables, corresponding to whether a random variable is valued in a countable subset or in an interval of real numbers. There are other important possibilities, especially in the theory of stochastic processes, wherein it is natural to consider random sequences or random functions. Sometimes a random variable is taken to be automatically valued in the real numbers, with more general random quantities instead being called random elements.
According to George Mackey, Pafnuty Chebyshev was the first person "to think systematically in terms of random variables".[3]
- ^ a b Blitzstein, Joe; Hwang, Jessica (2014). Introduction to Probability. CRC Press. ISBN 9781466575592.
- ^ Deisenroth, Marc Peter (2020). Mathematics for machine learning. A. Aldo Faisal, Cheng Soon Ong. Cambridge, United Kingdom: Cambridge University Press. ISBN 978-1-108-47004-9. OCLC 1104219401.
- ^ George Mackey (July 1980). "Harmonic analysis as the exploitation of symmetry – a historical survey". Bulletin of the American Mathematical Society. New Series. 3 (1).



