This article includes a list of general references, but it lacks sufficient corresponding inline citations. (December 2010) |
| Rhombic triacontahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | jD |
| Face type | V3.5.3.5 rhombus |
| Faces | 30 |
| Edges | 60 |
| Vertices | 32 |
| Vertices by type | 20{3}+12{5} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 144° |
| Properties | convex, face-transitive isohedral, isotoxal, zonohedron |
 Icosidodecahedron (dual polyhedron) |
 Net |

The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.
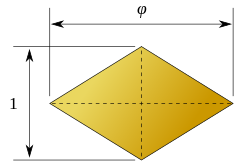 A face of the rhombic triacontahedron. The lengths of the diagonals are in the golden ratio. |

The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, φ, so that the acute angles on each face measure 2 arctan(1/φ) = arctan(2), or approximately 63.43°. A rhombus so obtained is called a golden rhombus.
Being the dual of an Archimedean solid, the rhombic triacontahedron is face-transitive, meaning the symmetry group of the solid acts transitively on the set of faces. This means that for any two faces, A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B.
The rhombic triacontahedron is somewhat special in being one of the nine edge-transitive convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron, and the rhombic dodecahedron.
The rhombic triacontahedron is also interesting in that its vertices include the arrangement of four Platonic solids. It contains ten tetrahedra, five cubes, an icosahedron and a dodecahedron. The centers of the faces contain five octahedra.
It can be made from a truncated octahedron by dividing the hexagonal faces into three rhombi:
