This article needs additional citations for verification. (March 2024) |
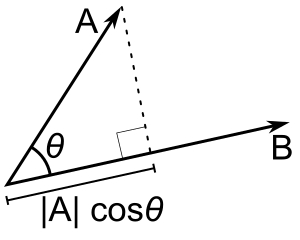

In mathematics, the scalar projection of a vector on (or onto) a vector also known as the scalar resolute of in the direction of is given by:
where the operator denotes a dot product, is the unit vector in the direction of is the length of and is the angle between and .[1]
The term scalar component refers sometimes to scalar projection, as, in Cartesian coordinates, the components of a vector are the scalar projections in the directions of the coordinate axes.
The scalar projection is a scalar, equal to the length of the orthogonal projection of on , with a negative sign if the projection has an opposite direction with respect to .
Multiplying the scalar projection of on by converts it into the above-mentioned orthogonal projection, also called vector projection of on .
- ^ Strang, Gilbert (2016). Introduction to linear algebra (5th ed.). Wellesley: Cambridge press. ISBN 978-0-9802327-7-6.









