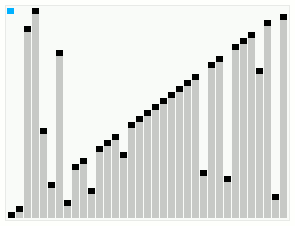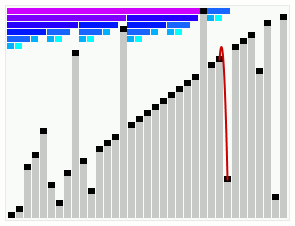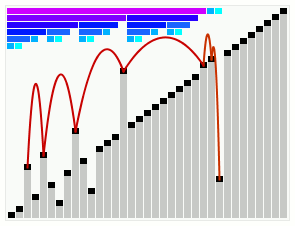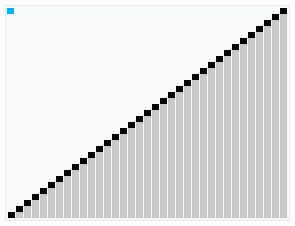
 Smoothsort operating on an array which is mostly in order. The bars across the top show the tree structure. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(n log n) |
| Best-case performance | O(n) |
| Average performance | O(n log n) |
| Worst-case space complexity | O(n) total, O(1) auxiliary |
| Optimal | When the data is already sorted |
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981.[1] Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation),[2] but it is not a stable sort.[3][self-published source?][4] The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.
- ^ Dijkstra, Edsger W. 16 Aug 1981 (EWD-796a) (PDF). E.W. Dijkstra Archive. Center for American History, University of Texas at Austin.
One can also raise the question why I have not chosen as available stretch lengths: ... 63 31 15 7 3 1 which seems attractive since each stretch can then be viewed as the postorder traversal of a balanced binary tree. In addition, the recurrence relation would be simpler. But I know why I chose the Leonardo numbers:
(transcription) - ^ Cite error: The named reference
hertelwas invoked but never defined (see the help page). - ^ Brown, Craig (21 Jan 2013). "Fastest In-Place Stable Sort". Code Project.[self-published source]
- ^ Eisenstat, David (13 September 2020). "Where is the smoothsort algorithm used?". Stack Overflow. Retrieved 2020-10-28.
Smoothsort is not stable, and stability is often more desirable than in-place in practice