Spherical segment

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (May 2024) (Learn how and when to remove this message)

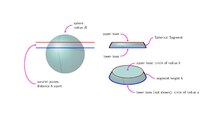
In geometry, a spherical segment is the solid defined by cutting a sphere or a ball with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum.

The surface of the spherical segment (excluding the bases) is called spherical zone.

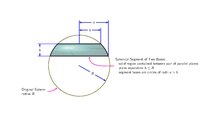
If the radius of the sphere is called R, the radii of the spherical segment bases are a and b, and the height of the segment (the distance from one parallel plane to the other) called h, then the volume of the spherical segment is

${\displaystyle V={\frac {\pi }{6}}h\left(3a^{2}+3b^{2}+h^{2}\right).}$

For the special case of the top plane being tangent to the sphere, we have ${\displaystyle b=0}$ and the solid reduces to a spherical cap.^[1]

The equation above for volume of the spherical segment can be arranged to

${\displaystyle V={\biggl [}\pi a^{2}\left({\frac {h}{2}}{\biggr )}\right]+{\biggl [}\pi b^{2}\left({\frac {h}{2}}{\biggr )}\right]+{\biggl [}{\frac {4}{3}}\pi \left({\frac {h}{2}}\right)^{3}{\biggr ]}}$

Thus, the segment volume equals the sum of three volumes: two right circular cylinders one of radius a and the second of radius b (both of height ${\displaystyle h/2}$) and a sphere of radius ${\displaystyle h/2}$.

The curved surface area of the spherical zone—which excludes the top and bottom bases—is given by

${\displaystyle A=2\pi Rh.}$