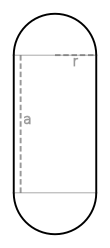


A stadium is a two-dimensional geometric shape constructed of a rectangle with semicircles at a pair of opposite sides.[1] The same shape is known also as a pill shape,[2] discorectangle,[3] obround,[4][5] or sausage body.[6]
The shape is based on a stadium, a place used for athletics and horse racing tracks.
A stadium may be constructed as the Minkowski sum of a disk and a line segment.[6] Alternatively, it is the neighborhood of points within a given distance from a line segment. A stadium is a type of oval. However, unlike some other ovals such as the ellipses, it is not an algebraic curve because different parts of its boundary are defined by different equations.
- ^ Weisstein, Eric W. "Stadium". MathWorld.
- ^ O'Hara, Michael J.; O'Leary, Dianne P. (April 2008). "Adiabatic theorem in the presence of noise". Physical Review A. 77 (4). American Physical Society (APS): 042319-1–042319-20. arXiv:0801.3872. doi:10.1103/physreva.77.042319.
- ^ Dzubiella, Joachim; Matthias Schmidt; Hartmut Löwen (2000). "Topological defects in nematic droplets of hard spherocylinders". Physical Review E. 62 (4): 5081–5091. arXiv:cond-mat/9906388. Bibcode:2000PhRvE..62.5081D. doi:10.1103/PhysRevE.62.5081. PMID 11089056. S2CID 31381033.
- ^ Ackermann, Kurt. "Obround - Punching Tools - VIP, Inc". www.vista-industrial.com. Retrieved 2016-04-29.
- ^ "Obround Level Gauge Glass : L.J. Star Incorporated". L.J.Star Incorporated. Archived from the original on 2016-04-22. Retrieved 2016-04-29.
- ^ a b Huang, Pingliang; Pan, Shengliang; Yang, Yunlong (2015). "Positive center sets of convex curves". Discrete & Computational Geometry. 54 (3): 728–740. doi:10.1007/s00454-015-9715-9. MR 3392976.