Standard basis

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (July 2016) (Learn how and when to remove this message)

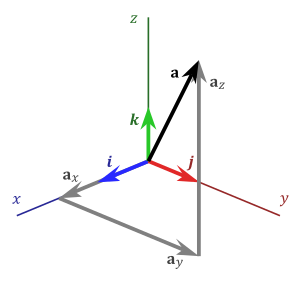
In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as ${\displaystyle \mathbb {R} ^{n}}$ or ${\displaystyle \mathbb {C} ^{n}}$) is the set of vectors, each of whose components are all zero, except one that equals 1.^[1] For example, in the case of the Euclidean plane ${\displaystyle \mathbb {R} ^{2}}$ formed by the pairs (x, y) of real numbers, the standard basis is formed by the vectors $${\displaystyle \mathbf {e} _{x}=(1,0),\quad \mathbf {e} _{y}=(0,1).}$$ Similarly, the standard basis for the three-dimensional space ${\displaystyle \mathbb {R} ^{3}}$ is formed by vectors $${\displaystyle \mathbf {e} _{x}=(1,0,0),\quad \mathbf {e} _{y}=(0,1,0),\quad \mathbf {e} _{z}=(0,0,1).}$$

Here the vector e_x points in the x direction, the vector e_y points in the y direction, and the vector e_z points in the z direction. There are several common notations for standard-basis vectors, including {e_x, e_y, e_z}, {e₁, e₂, e₃}, {i, j, k}, and {x, y, z}. These vectors are sometimes written with a hat to emphasize their status as unit vectors (standard unit vectors).

These vectors are a basis in the sense that any other vector can be expressed uniquely as a linear combination of these.^[2] For example, every vector v in three-dimensional space can be written uniquely as $${\displaystyle v_{x}\,\mathbf {e} _{x}+v_{y}\,\mathbf {e} _{y}+v_{z}\,\mathbf {e} _{z},}$$ the scalars ${\displaystyle v_{x}}$, ${\displaystyle v_{y}}$, ${\displaystyle v_{z}}$ being the scalar components of the vector v.

In the n-dimensional Euclidean space ${\displaystyle \mathbb {R} ^{n}}$, the standard basis consists of n distinct vectors $${\displaystyle \{\mathbf {e} _{i}:1\leq i\leq n\},}$$ where e_i denotes the vector with a 1 in the ith coordinate and 0's elsewhere.

Standard bases can be defined for other vector spaces, whose definition involves coefficients, such as polynomials and matrices. In both cases, the standard basis consists of the elements of the space such that all coefficients but one are 0 and the non-zero one is 1. For polynomials, the standard basis thus consists of the monomials and is commonly called monomial basis. For matrices ${\displaystyle {\mathcal {M}}_{m\times n}}$, the standard basis consists of the m×n-matrices with exactly one non-zero entry, which is 1. For example, the standard basis for 2×2 matrices is formed by the 4 matrices $${\displaystyle \mathbf {e} _{11}={\begin{pmatrix}1&0\\0&0\end{pmatrix}},\quad \mathbf {e} _{12}={\begin{pmatrix}0&1\\0&0\end{pmatrix}},\quad \mathbf {e} _{21}={\begin{pmatrix}0&0\\1&0\end{pmatrix}},\quad \mathbf {e} _{22}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.}$$