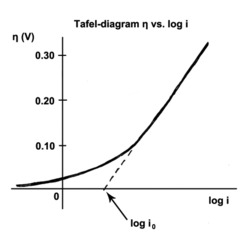
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential.[1] The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.
It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction.[2][circular reference]
Where an electrochemical reaction occurs in two half reactions on separate electrodes, the Tafel equation is applied to each electrode separately. On a single electrode the Tafel equation can be stated as:
| (1) |
where
- the plus sign under the exponent refers to an anodic reaction,[3] and a minus sign to a cathodic reaction[4][circular reference],[5]
- : overpotential, [V]
- : Tafel slope", [V]
- : current density, [A/m2]
- : "exchange current density", [A/m2].
A verification plus further explanation for this equation can be found here.[6] The Tafel equation is an approximation of the Butler–Volmer equation in the case of .
"[ The Tafel equation ] assumes that the concentrations at the electrode are practically equal to the concentrations in the bulk electrolyte, allowing the current to be expressed as a function of potential only. In other words, it assumes that the electrode mass transfer rate is much greater than the reaction rate, and that the reaction is dominated by the slower chemical reaction rate ".[7][circular reference]
Also, at a given electrode the Tafel equation assumes that the reverse half reaction rate is negligible compared to the forward reaction rate.
- ^ Bard, A. J.; Faulkner, L. R. “Electrochemical Methods. Fundamentals and Applications” 2nd Ed. Wiley, New York. 2001. ISBN 0-471-04372-9
- ^ "Applicability".
- ^ "Tafel Slope for Anodic Reaction from Tafel Equation Calculator | Calculate Tafel Slope for Anodic Reaction from Tafel Equation". www.calculatoratoz.com. Retrieved 2024-05-28.
- ^ "Limiting cases of Butler–Volmer equation".
- ^ "Tafel Slope for Cathodic Reaction from Tafel Equation Calculator | Calculate Tafel Slope for Cathodic Reaction from Tafel Equation". www.calculatoratoz.com. Retrieved 2024-05-28.
- ^ "Verification of Tafel Equation".
- ^ "Applicability".






