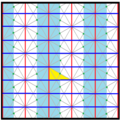
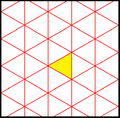
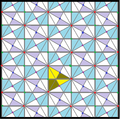
In geometry, the [6,3], (*632) symmetry group is bounded by mirrors meeting with angles of 30, 60, and 90 degrees. There are a number of small index subgroups constructed by mirror removal and alternation. h[6,3] = [1+,6,3] creates [3[3]], (*333) symmetry, shown as red mirror lines. Removing mirrors at the order-3 point creates [6,3+], 3*3 symmetry, index 2. Removing all mirrors creates [6,3]+ (632) subgroup, index 2. The communtator subgroup is [1+,6,3+], (333) symmetry, index 4. An index 6 subgroup constructed as [6,3*], also becomes (*333), shown in blue mirror lines, and which has its own (333) rotational symmetry, index 12.
| Small index subgroups [6,3] (*632) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | 1 | 2 | 3 | 6 | |||||||
| Diagram | 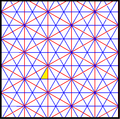
|

|

|
|

|
| |||||
| Intl (orb.) Coxeter |
p6m (*632) [6,3] = |
p3m1 (*333) [1+,6,3] = |
p31m (3*3) [6,3+] = |
cmm (2*22) | pmm (*2222) | p3m1 (*333) [6,3*] = | |||||
| Direct subgroups | |||||||||||
| Index | 2 | 4 | 6 | 12 | |||||||
| Diagram | 
|

|
|
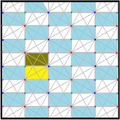
|

| ||||||
| Intl (orb.) Coxeter |
p6 (632) [6,3]+ = |
p3 (333) [1+,6,3+] = |
p2 (2222) | p2 (2222) | p3 (333) [1+,6,3*] = | ||||||