| Alternated cubic honeycomb | |
|---|---|
 
| |
| Type | Uniform honeycomb |
| Family | Alternated hypercubic honeycomb Simplectic honeycomb |
| Indexing[1] | J21,31,51, A2 W9, G1 |
| Schläfli symbols | h{4,3,4} {3[4]} ht0,3{4,3,4} h{4,4}h{∞} ht0,2{4,4}h{∞} h{∞}h{∞}h{∞} s{∞}s{∞}s{∞} |
| Coxeter diagrams | |
| Cells | {3,3} {3,4} |
| Faces | triangle {3} |
| Edge figure | [{3,3}.{3,4}]2 (rectangle) |
| Vertex figure |  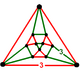  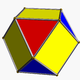 (cuboctahedron) |
| Symmetry group | Fm3m (225) |
| Coxeter group | , [4,31,1] |
| Dual | Dodecahedrille rhombic dodecahedral honeycomb Cell: 
|
| Properties | vertex-transitive, edge-transitive, quasiregular honeycomb |
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
Other names include half cubic honeycomb, half cubic cellulation, or tetragonal disphenoidal cellulation. John Horton Conway calls this honeycomb a tetroctahedrille, and its dual a dodecahedrille.
R. Buckminster Fuller combines the two words octahedron and tetrahedron into octet truss, a rhombohedron consisting of one octahedron (or two square pyramids) and two opposite tetrahedra.
It is vertex-transitive with 8 tetrahedra and 6 octahedra around each vertex. It is edge-transitive with 2 tetrahedra and 2 octahedra alternating on each edge.
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
It is part of an infinite family of uniform honeycombs called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of demihypercube and cross-polytope facets. It is also part of another infinite family of uniform honeycombs called simplectic honeycombs.
In this case of 3-space, the cubic honeycomb is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended Schläfli symbol h{4,3,4} as containing half the vertices of the {4,3,4} cubic honeycomb.
There is a similar honeycomb called gyrated tetrahedral-octahedral honeycomb which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra.
The tetrahedral-octahedral honeycomb can have its symmetry doubled by placing tetrahedra on the octahedral cells, creating a nonuniform honeycomb consisting of tetrahedra and octahedra (as triangular antiprisms). Its vertex figure is an order-3 truncated triakis tetrahedron. This honeycomb is the dual of the triakis truncated tetrahedral honeycomb, with triakis truncated tetrahedral cells.
- ^ For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
