Three-body problem

This article is about the physics theory. For other uses, see Three-body problem (disambiguation).
Approximate trajectories of three identical bodies located at the vertices of a scalene triangle and having zero initial velocities. The center of mass, in accordance with the law of conservation of momentum, remains in place.

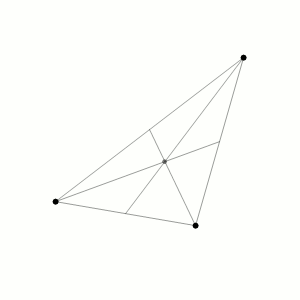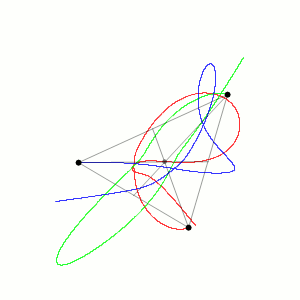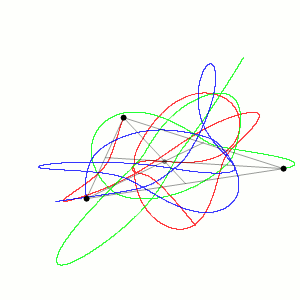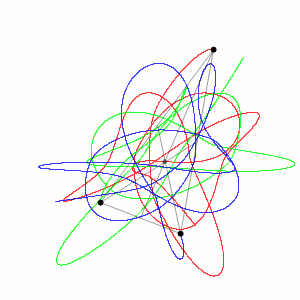
In physics, specifically classical mechanics, the three-body problem is to take the initial positions and velocities (or momenta) of three point masses that orbit each other in space and calculate their subsequent trajectories using Newton's laws of motion and Newton's law of universal gravitation.[1]

Unlike the two-body problem, the three-body problem has no general closed-form solution, meaning there is no equation that always solves it.[1] When three bodies orbit each other, the resulting dynamical system is chaotic for most initial conditions. Because there are no solvable equations for most three-body systems, the only way to predict the motions of the bodies is to estimate them using numerical methods.

The three-body problem is a special case of the n-body problem. Historically, the first specific three-body problem to receive extended study was the one involving the Earth, the Moon, and the Sun.[2] In an extended modern sense, a three-body problem is any problem in classical mechanics or quantum mechanics that models the motion of three particles.

  1. ^ a b Barrow-Green, June (2008). "The Three-Body Problem". In Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.). The Princeton Companion to Mathematics. Princeton University Press. pp. 726–728.
  2. ^ "Historical Notes: Three-Body Problem". Retrieved 19 July 2017.