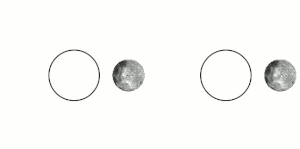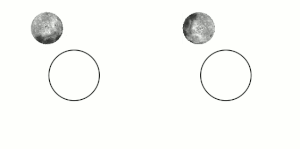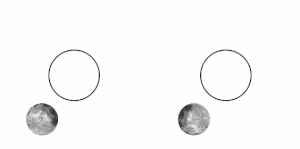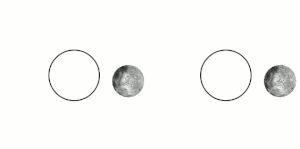
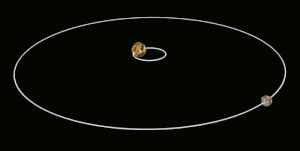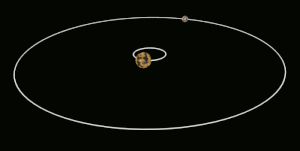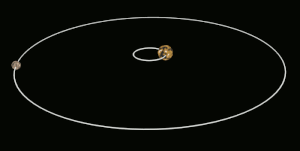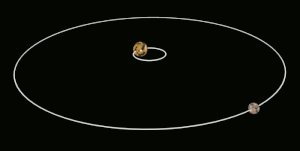
Tidal locking

Tidal locking results in the Moon rotating about its axis in about the same time it takes to orbit Earth. Except for libration, this results in the Moon keeping the same face turned toward Earth, as seen in the left figure. If the Moon were not rotating at all, it would alternately show its near and far sides to Earth, while moving around Earth in orbit, as shown in the right figure. The Moon is shown in polar view, and is not drawn to scale.
A side view of the Pluto–Charon system. Pluto and Charon are tidally locked to each other. Charon is massive enough that the barycenter of Pluto's system lies outside of Pluto; thus, Pluto and Charon are sometimes considered to be a binary system.

Tidal locking between a pair of co-orbiting astronomical bodies occurs when one of the objects reaches a state where there is no longer any net change in its rotation rate over the course of a complete orbit. In the case where a tidally locked body possesses synchronous rotation, the object takes just as long to rotate around its own axis as it does to revolve around its partner. For example, the same side of the Moon always faces Earth, although there is some variability because the Moon's orbit is not perfectly circular. Usually, only the satellite is tidally locked to the larger body.[1] However, if both the difference in mass between the two bodies and the distance between them are relatively small, each may be tidally locked to the other; this is the case for Pluto and Charon, as well as for Eris and Dysnomia. Alternative names for the tidal locking process are gravitational locking,[2] captured rotation, and spin–orbit locking.

The effect arises between two bodies when their gravitational interaction slows a body's rotation until it becomes tidally locked. Over many millions of years, the interaction forces changes to their orbits and rotation rates as a result of energy exchange and heat dissipation. When one of the bodies reaches a state where there is no longer any net change in its rotation rate over the course of a complete orbit, it is said to be tidally locked.[3] The object tends to stay in this state because leaving it would require adding energy back into the system. The object's orbit may migrate over time so as to undo the tidal lock, for example, if a giant planet perturbs the object.

There is ambiguity in the use of the terms 'tidally locked' and 'tidal locking', in that some scientific sources use it to refer exclusively to 1:1 synchronous rotation (e.g. the Moon), while others include non-synchronous orbital resonances in which there is no further transfer of angular momentum over the course of one orbit (e.g. Mercury).[4] In Mercury's case, the planet completes three rotations for every two revolutions around the Sun, a 3:2 spin–orbit resonance. In the special case where an orbit is nearly circular and the body's rotation axis is not significantly tilted, such as the Moon, tidal locking results in the same hemisphere of the revolving object constantly facing its partner.[3][4][5] Regardless of which definition of tidal locking is used, the hemisphere that is visible changes slightly due to variations in the locked body's orbital velocity and the inclination of its rotation axis over time.

  1. ^ "When Will Earth Lock to the Moon?". Universe Today. 2016-04-12. Archived from the original on 2016-09-23. Retrieved 2017-01-02.
  2. ^ Cite error: The named reference Clouse_et_al_2022 was invoked but never defined (see the help page).
  3. ^ a b Barnes, Rory, ed. (2010). Formation and Evolution of Exoplanets. John Wiley & Sons. p. 248. ISBN 978-3527408962. Archived from the original on 2023-08-06. Retrieved 2016-08-16.
  4. ^ a b Heller, R.; Leconte, J.; Barnes, R. (April 2011). "Tidal obliquity evolution of potentially habitable planets". Astronomy & Astrophysics. 528: 16. arXiv:1101.2156. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809. S2CID 118784209. A27.
  5. ^ Mahoney, T. J. (2013). Mercury. Springer Science & Business Media. ISBN 978-1461479512. Archived from the original on 2023-08-06. Retrieved 2018-04-20.