In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.[1][2] This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality.[3] If a, b, and c are the lengths of the sides of a triangle then the triangle inequality states that
with equality only in the degenerate case of a triangle with zero area.
In Euclidean geometry and some other geometries, the triangle inequality is a theorem about vectors and vector lengths (norms):
where the length of the third side has been replaced by the length of the vector sum u + v. When u and v are real numbers, they can be viewed as vectors in , and the triangle inequality expresses a relationship between absolute values.
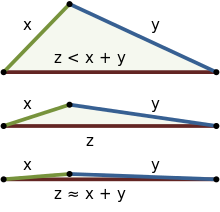
In Euclidean geometry, for right triangles the triangle inequality is a consequence of the Pythagorean theorem, and for general triangles, a consequence of the law of cosines, although it may be proved without these theorems. The inequality can be viewed intuitively in either or . The figure at the right shows three examples beginning with clear inequality (top) and approaching equality (bottom). In the Euclidean case, equality occurs only if the triangle has a 180° angle and two 0° angles, making the three vertices collinear, as shown in the bottom example. Thus, in Euclidean geometry, the shortest distance between two points is a straight line.
In spherical geometry, the shortest distance between two points is an arc of a great circle, but the triangle inequality holds provided the restriction is made that the distance between two points on a sphere is the length of a minor spherical line segment (that is, one with central angle in [0, π]) with those endpoints.[4][5]
The triangle inequality is a defining property of norms and measures of distance. This property must be established as a theorem for any function proposed for such purposes for each particular space: for example, spaces such as the real numbers, Euclidean spaces, the Lp spaces (p ≥ 1), and inner product spaces.
- ^ Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html
- ^ Mohamed A. Khamsi; William A. Kirk (2001). "§1.4 The triangle inequality in Rn". An introduction to metric spaces and fixed point theory. Wiley-IEEE. ISBN 0-471-41825-0.
- ^ for instance, Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., p. 246, ISBN 0-7167-0456-0
- ^ Oliver Brock; Jeff Trinkle; Fabio Ramos (2009). Robotics: Science and Systems IV. MIT Press. p. 195. ISBN 978-0-262-51309-8.
- ^ Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to hyperbolic geometry. Springer. p. 17. ISBN 0-387-94339-0.





