Umbilical point

In the differential geometry of surfaces in three dimensions, umbilics or umbilical points are points on a surface that are locally spherical. At such points the normal curvatures in all directions are equal, hence, both principal curvatures are equal, and every tangent vector is a principal direction. The name "umbilic" comes from the Latin umbilicus (navel).

Umbilic points generally occur as isolated points in the elliptical region of the surface; that is, where the Gaussian curvature is positive.

The sphere is the only surface with non-zero curvature where every point is umbilic. A flat umbilic is an umbilic with zero Gaussian curvature. The monkey saddle is an example of a surface with a flat umbilic and on the plane every point is a flat umbilic. A closed surface topologically equivalent to a torus may or may not have zero umbilics, but every closed surface of nonzero Euler characteristic, embedded smoothly into Euclidean space, has at least one umbilic. An unproven conjecture of Constantin Carathéodory states that every smooth surface topologically equivalent to the sphere has at least two umbilics.^[1]

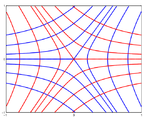
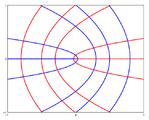
The three main types of umbilic points are elliptical umbilics, parabolic umbilics and hyperbolic umbilics. Elliptical umbilics have the three ridge lines passing through the umbilic and hyperbolic umbilics have just one. Parabolic umbilics are a transitional case with two ridges one of which is singular. Other configurations are possible for transitional cases. These cases correspond to the D₄⁻, D₅ and D₄⁺ elementary catastrophes of René Thom's catastrophe theory.

Umbilics can also be characterised by the pattern of the principal direction vector field around the umbilic which typically form one of three configurations: star, lemon, and lemonstar (or monstar). The index of the vector field is either −½ (star) or ½ (lemon, monstar). Elliptical and parabolic umbilics always have the star pattern, whilst hyperbolic umbilics can be star, lemon, or monstar. This classification was first due to Darboux and the names come from Hannay.^[2]

For surfaces with genus 0 with isolated umbilics, e.g. an ellipsoid, the index of the principal direction vector field must be 2 by the Poincaré–Hopf theorem. Generic genus 0 surfaces have at least four umbilics of index ½. An ellipsoid of revolution has two non-generic umbilics each of which has index 1.^[3]

• configurations of lines of curvature near umbilics
• 
  Star
• 
  Monstar
• 
  Lemon