Variational autoencoder

The basic scheme of a variational autoencoder. The model receives as input. The encoder compresses it into the latent space. The decoder receives as input the information sampled from the latent space and produces as similar as possible to .
Part of a series on
Machine learning
and data mining
Paradigms
Problems
Clustering
Dimensionality reduction
Structured prediction
Anomaly detection
Artificial neural network
Reinforcement learning
Learning with humans
Model diagnostics
Mathematical foundations
Journals and conferences
Related articles

In machine learning, a variational autoencoder (VAE) is an artificial neural network architecture introduced by Diederik P. Kingma and Max Welling.[1] It is part of the families of probabilistic graphical models and variational Bayesian methods.[2]

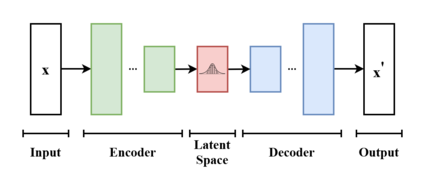
In addition to being seen as an autoencoder neural network architecture, variational autoencoders can also be studied within the mathematical formulation of variational Bayesian methods, connecting a neural encoder network to its decoder through a probabilistic latent space (for example, as a multivariate Gaussian distribution) that corresponds to the parameters of a variational distribution.

Thus, the encoder maps each point (such as an image) from a large complex dataset into a distribution within the latent space, rather than to a single point in that space. The decoder has the opposite function, which is to map from the latent space to the input space, again according to a distribution (although in practice, noise is rarely added during the decoding stage). By mapping a point to a distribution instead of a single point, the network can avoid overfitting the training data. Both networks are typically trained together with the usage of the reparameterization trick, although the variance of the noise model can be learned separately.[citation needed]

Although this type of model was initially designed for unsupervised learning,[3][4] its effectiveness has been proven for semi-supervised learning[5][6] and supervised learning.[7]

  1. ^ Kingma, Diederik P.; Welling, Max (2022-12-10). "Auto-Encoding Variational Bayes". arXiv:1312.6114 [stat.ML].
  2. ^ Pinheiro Cinelli, Lucas; et al. (2021). "Variational Autoencoder". Variational Methods for Machine Learning with Applications to Deep Networks. Springer. pp. 111–149. doi:10.1007/978-3-030-70679-1_5. ISBN 978-3-030-70681-4. S2CID 240802776.
  3. ^ Dilokthanakul, Nat; Mediano, Pedro A. M.; Garnelo, Marta; Lee, Matthew C. H.; Salimbeni, Hugh; Arulkumaran, Kai; Shanahan, Murray (2017-01-13). "Deep Unsupervised Clustering with Gaussian Mixture Variational Autoencoders". arXiv:1611.02648 [cs.LG].
  4. ^ Hsu, Wei-Ning; Zhang, Yu; Glass, James (December 2017). "Unsupervised domain adaptation for robust speech recognition via variational autoencoder-based data augmentation". 2017 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU). pp. 16–23. arXiv:1707.06265. doi:10.1109/ASRU.2017.8268911. ISBN 978-1-5090-4788-8. S2CID 22681625.
  5. ^ Ehsan Abbasnejad, M.; Dick, Anthony; van den Hengel, Anton (2017). Infinite Variational Autoencoder for Semi-Supervised Learning. pp. 5888–5897.
  6. ^ Xu, Weidi; Sun, Haoze; Deng, Chao; Tan, Ying (2017-02-12). "Variational Autoencoder for Semi-Supervised Text Classification". Proceedings of the AAAI Conference on Artificial Intelligence. 31 (1). doi:10.1609/aaai.v31i1.10966. S2CID 2060721.
  7. ^ Kameoka, Hirokazu; Li, Li; Inoue, Shota; Makino, Shoji (2019-09-01). "Supervised Determined Source Separation with Multichannel Variational Autoencoder". Neural Computation. 31 (9): 1891–1914. doi:10.1162/neco_a_01217. PMID 31335290. S2CID 198168155.