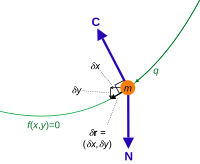
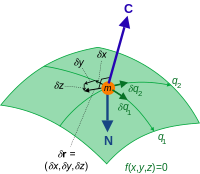
In analytical mechanics, a branch of applied mathematics and physics, a virtual displacement (or infinitesimal variation) shows how the mechanical system's trajectory can hypothetically (hence the term virtual) deviate very slightly from the actual trajectory of the system without violating the system's constraints.[1][2][3]: 263 For every time instant is a vector tangential to the configuration space at the point The vectors show the directions in which can "go" without breaking the constraints.
For example, the virtual displacements of the system consisting of a single particle on a two-dimensional surface fill up the entire tangent plane, assuming there are no additional constraints.
If, however, the constraints require that all the trajectories pass through the given point at the given time i.e. then
- ^ Takhtajan, Leon A. (2017). "Part 1. Classical Mechanics". Classical Field Theory (PDF). Department of Mathematics, Stony Brook University, Stony Brook, NY.
- ^ Goldstein, H.; Poole, C. P.; Safko, J. L. (2001). Classical Mechanics (3rd ed.). Addison-Wesley. p. 16. ISBN 978-0-201-65702-9.
- ^ Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.