
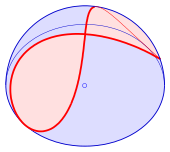
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles (a diameter) of the sphere (see diagram). Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.[1][2]
The orthographic projection of Viviani's curve onto a plane perpendicular to the line through the crossing point and the sphere center is the lemniscate of Gerono, while the stereographic projection is a hyperbola or the lemniscate of Bernoulli, depending on which point on the same line is used to project.[3]
In 1692 Viviani solved the following task: Cut out of a half sphere (radius ) two windows, such that the remaining surface (of the half sphere) can be squared, i.e. a square with the same area can be constructed using only compasses and ruler. His solution has an area of (see below).
- ^ Kuno Fladt: Analytische Geometrie spezieller Flächen und Raumkurven. Springer-Verlag, 2013, ISBN 3322853659, 9783322853653, p. 97.
- ^ K. Strubecker: Vorlesungen der Darstellenden Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, p. 250.
- ^ Costa, Luisa Rossi; Marchetti, Elena (2005), "Mathematical and Historical Investigation on Domes and Vaults", in Weber, Ralf; Amann, Matthias Albrecht (eds.), Aesthetics and architectural composition : proceedings of the Dresden International Symposium of Architecture 2004, Mammendorf: Pro Literatur, pp. 73–80.

