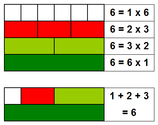
Mersenne primes and perfect numbers are two deeply interlinked types of natural numbers in number theory. Mersenne primes, named after the friar Marin Mersenne, are prime numbers that can be expressed as 2p − 1 for some positive integer p. For example, 3 is a Mersenne prime as it is a prime number and is expressible as 22 − 1. Perfect numbers are natural numbers that equal the sum of their positive proper divisors (all divisors excluding the number itself). There is a one-to-one correspondence between the Mersenne primes and the even perfect numbers. This is due to the Euclid–Euler theorem, partially proved by Euclid and completed by Leonhard Euler: even numbers are perfect if and only if they can be expressed in the form 2p − 1 × (2p − 1), where 2p − 1 is a Mersenne prime. (Full list...)