Wind triangle

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (July 2020) (Learn how and when to remove this message)

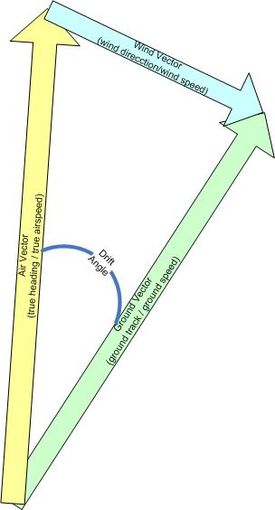
In air navigation, the wind triangle is a graphical representation of the relationship between aircraft motion and wind. It is used extensively in dead reckoning navigation.

The wind triangle is a vector diagram, with three vectors.

• The air vector represents the motion of the aircraft through the airmass. It is described by true airspeed and true heading.
• The wind vector represents the motion of the airmass over the ground. It is described by wind speed and the inverse of wind direction. Note that by convention wind direction is given as the direction the wind is from. In a vector diagram such as the wind triangle, wind direction must be stated as the direction the wind is blowing to, or 180 degrees different from the convention.
• The ground vector represents the motion of the aircraft over the ground. It is described by ground track and ground speed. The ground vector is the resultant of algebraically adding the air vector and the wind vector.

The wind triangle describes the relationships among the quantities used in air navigation. When two of the three vectors, or four of the six components, are known, the remaining quantities can be derived. The three principal types of problems to solve are:

1. Solve for the ground vector. This type of problem arises when true heading and true airspeed are known by reading the flight instruments and when wind direction and speed are known from either the meteorological forecast or from determination in flight.
2. Solve for the wind vector. This type of problem arises when determination of heading and true airspeed can be done by reading the flight instruments and ground track and ground speed can be found either by measuring the direction and distance between two established points of the aircraft or by determining the drift angle and ground speed by reference to the ground.
3. Solve for true heading and ground speed. This type of problem arises during flight planning or during a flight, when there is a need to determine a true heading to fly and a ground speed with which to compute an estimated time of arrival.

The traditional method of solving wind triangle equations is graphical. The known vectors are drawn to scale and in the proper direction on an aeronautical chart, using protractor and dividers. The unknown quantities are read from the chart using the same tools. Alternatively, the E6B flight computer (a circular slide rule with a translucent "wind face" on which to plot the vectors) can be used to graphically solve the wind triangle equations.

On aircraft equipped with advanced navigation equipment, the wind triangle is often solved within the flight management system, (FMS) using inputs from the air data computer (ADC), inertial navigation system (INS), global positioning system (GPS), and other instruments, (VOR), (DME), (ADF). The pilot simply reads the solution provided to them.