Zero-symmetric graph

18-vertex zero-symmetric graph
The smallest zero-symmetric graph, with 18 vertices and 27 edges
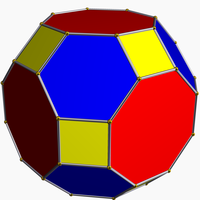
Truncated cuboctahedron
The truncated cuboctahedron, a zero-symmetric polyhedron
Graph families defined by their automorphisms
distance-transitive → distance-regular ← strongly regular
↓
symmetric (arc-transitive) ← t-transitive, t ≥ 2 skew-symmetric
↓
(if connected)
vertex- and edge-transitive 		→ edge-transitive and regular → edge-transitive
↓ ↓ ↓
vertex-transitive → regular → (if bipartite)
biregular
↑
Cayley graph ← zero-symmetric asymmetric

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.[1]

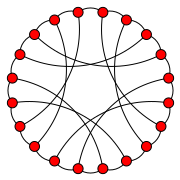
The smallest zero-symmetric graph with two edge orbits

The name for this class of graphs was coined by R. M. Foster in a 1966 letter to H. S. M. Coxeter.[2] In the context of group theory, zero-symmetric graphs are also called graphical regular representations of their symmetry groups.[3]

  1. ^ Coxeter, Harold Scott MacDonald; Frucht, Roberto; Powers, David L. (1981), Zero-symmetric graphs, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London, ISBN 0-12-194580-4, MR 0658666
  2. ^ Coxeter, Frucht & Powers (1981), p. ix.
  3. ^ Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, p. 66, ISBN 9780521529037.